종이비행기 실험을 통한 항공기의 무게 중심과 공력중심에 대한 탐구
함께 연구한 아이들 - 김포 장기고 주영훈(3) 황예성(1), 푸른솔중 윤세훈(3)

Ⅰ. 서론
종이비행기에 적용되는 다른 항공역학적 요소에 대해 공부해 보다 과학하는 청소년활동가 최누리 씨의 ‘활공하는 종이비행기의 구조 안전성과 비행거리에 대한 실험’ 발표영상을 접했다. 이 실험에서는 a4 용지 크기의 종이로 종이비행기를 접은 다음, 무게중심과 공력중심의 길이를 다르게 하여 가장 멀리 가는 길이를 알아내었다. 그런데, 이 영상을 보던 중 “비행기 전체 길이에 대한 공력중심과 무게중심 사이의 길이의 비가 몇 대 몇인 비행기가 가장 멀리 비행할 수 있을까”에 대한 궁금증이 생겼다. 그래서 종이비행기에서 가장 멀리 비행할 수 있는 공력중심과 무게중심 사이의 길이의 비를 구하는 실험을 진행하게 되었다.
Ⅱ. 이론적배경
무게중심과 공력중심
1) 항공기의 무게중심과 공력중심
물리학에서 말하는 무게중심은 중력에 의한 알짜 torque가 0인 점이다. 즉 물체의 각 부분에 작용하는 중력의 합력이 작용하는 지점을 말한다. 항공역학에서 무게중심이란 항공기의 총중량이 집중되는 지점/항공기의 모멘트의 합이 0이 되는 지점으로 종적, 횡적으로 평형이 되는 지점에 위치해야 한다. 각 부분에 걸리는 모멘트의 총 합계를 총 중량으로 나누어서 구할 수 있다. MAC(평균공력시위)를 이용해 무게중심의 위치를 나타낸다. 평균공력시위(MAC)이란 날개의 공기역학적 특성을 대표하는 시위, 항공기의 날개 앞전부터 뒷전까지의 평균 길이를 의미한다.
2) 종이비행기에서의 공력중심
공력중심은 에어포일의 피칭 모멘트의 받음각이 변하여도 피칭 모멘트가 일정한 기준점으로 일반적으로 날개 시위의 25%MAC 지점에 위치한다. 압력중심의 경우 방향이 바뀔 때마다 위치가 변해 힘과 모멘트를 계산하기 힘들기 때문에 공력중심을 임의로 정하여 계산한다. 공력중심은 무게중심과 압력중심을 계산함으로써 정의할 수 있으나 문헌상에서 종이비행기의 공력중심 계산법이 소개되어 있다.
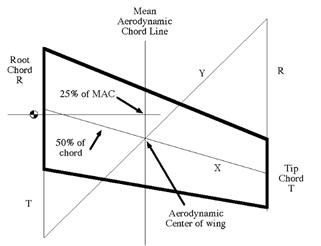
그림 . 종이비행기에서의 공력중심 계산(출처: 최누리, 제 17회 NYSC 우주과학 포럼)
Ⅲ. 연구방법
종이의 비율이 일정하다 하고, 일정한 비율의 종이로 만들어진 종이 비행기가 있을 때, 공력중심과 무게 중심 차이의 비율에 따라서 움직인 거리가 최적화된 비율이 있다. 라는 가설에 따라서 a4용지와 b4용지, a3용지로 세가지 실험을 했다.
실험 1. A4 용지로 접은 종이비행기에서 비행거리가 가장 길게 나타나는 무게중심과 공력중심의 차이 지점 찾기
1) 종이비행기 제작 및 무게중심 찾기
(1) A4종이 비행기를 5개 만든다.
(2) 접을 때에는 a4용지를 세로로 절반을 접었다 핀다.
(3) 아래 양쪽을 45도로 접고 아래부분을 위로 접어 올린다. (이때 접는 높이에 따라 비행기의 무게중심이 바뀌는데 3cm로 높이를 정했다.)
(4) 아래 양쪽을 다시 접고 가운데를 접는다.
(5) 전체를 반으로 접고 대각선 방향으로 반으로 접는다.
(6) 날개 중간에 테이프를 붙인다.
(7) 무게중심은 실에 테이프를 붙여서 비행기 위쪽에 붙여보면서 날개쪽 과 뿌리 쪽을 이은 선이 수평이 될 때까지 실험적으로 측정한다. 이 때 A4용지로 만든 종이비행기는 뿌리 쪽으로부터 9cm 지점에 무게중심이 있다.
여기에서 종이비행기 5개 모두 날개 크기, 모양 등을 똑같이 했지만 첫 번째 종이비행기를 기준으로 해서 공력중심은 계속 똑같은 위치에 두고 무게중심을 1cm씩 늘리고 줄인다. 그래서 a4용지로 했을 때는 공력중심과 무게중심 차이가 각각 1cm, 2cm, 3cm, 4cm, 5cm 로 되었다. 이 차이에 따라서 무게가 또 바뀌어서 클립을 이용해서 비행기의 앞 뒤 무게를 맞춘다. 1, 2 cm일때는 클립을 2개 앞에다 달았고 4, 5cm일때는 뒤쪽에 클립 4개를 달아서 무게를 맞췄다.
실험 2. B4 용지로 접은 종이비행기에서 비행거리가 가장 길게 나타나는 무게중심과 공력중심의 차이 지점 찾기
(1) 실험 1과 같이 B4종이비행기도 5개 만든다.
(2) 실험 1과 같은 방식으로 공력중심과 무게중심을 구한다. 무게중심과 공력중심의 차이는 각각 2.5cm, 3.5cm, 4.5cm, 5.5cm, 6.5cm로 나온다. 이도 똑같이 클립을 2.5cm와 3.5cm 일 때는 2개를 앞에다가 달고 5.5cm와 6.5cm에는 4개를 달아줘서 무게를 맞췄다.
실험 3. A3 용지로 접은 종이비행기에서 비행거리가 가장 길게 나타나는 무게중심과 공력중심의 차이 지점 찾기
(1) 실험 1,2와 같이 A3종이비행기도 5개 만든다.
(2) 실험 1, 2와 같은 방식으로 공력중심과 무게중심을 구한다. 무게중심과 공력중심의 차이는 각각 3cm, 4cm, 5cm, 6cm, 7cm로 나온다. 이도 똑같이 클립을 3cm와 4cm 일 때는 2개를 앞에다가 달고 5.5cm와 6.5cm에는 6개를 달아줘서 무게를 맞췄다.
실험 4. 두 종이비행기에서의 비행거리 측정
A4용지 비행기 5개와 B4용지 비행기 5개와 A3 용지 비행기 5개를 각각 5번씩 날려서 동일한 사람이 동일한 각도로 던져서 비행거리를 측정했다.
Ⅳ. 연구결과

그림 . A4용지로 접은 종이비행기에서 무게중심과 공력중심 사이 길이에 따른 비행거리 결과
A4용지로 접은 종이비행기 5개 중, 무게중심과 공력중심 사이의 길이가 3cm인 종이비행기가 평균적으로 가장 멀리 비행하였다.그러나 네 번째 비행기와 마지막 비행기는 비행 도중 공중에서 한 바퀴를 돌거나, 비행 궤적이 아래 그림에 나온 것 같은 경우가 많았다.

그림 . 무게중심과 공력중심의 차이가 길 때 나타나는 불안정한 비행궤도의 사례
결론적으로 A4용지로 만든 종이비행기에서는 무게중심과 공력중심 사이의 길이가 3cm인 비행기가 평균적으로 가장 멀리 비행하였다. 그리고 A4용지로 만든 종이비행기의 전체 길이의 무게중심과 공력중심 사이의 길이에 대한 비율은 (비행기 길이):(두 중심사이의 길이)= 5.6 : 1 이 나왔다.

그림 . B4용지로 접은 종이비행기에서 무게중심과 공력중심 사이 길이에 따른 비행거리 결과
B4 용지로 접은 종이비행기 5가지 사이에서 무게중심과 공력중심 사이의 길이가 4.5cm인 비행기가 가장 멀리 비행하였다. 그러나 두 중심 사이의 길이가 5.5cm, 6.5cm인 비행기들은 비행할 때 A4용지로 만든 비행기 중 4번째, 마지막 비행기처럼 비행 궤도를 보이거나 비행 도중 공중제비를 도는 경우가 많았다.

그림14. A3용지로 접은 종이비행기에서 무게중심과 공력중심 사이 길이에 따른 비행거리 결과
A3 용지로 만든 종이비행기에서는 무게중심과 공력중심 사이의 길이가 5cm인 비행기가 평균적으로 가장 멀리 날았다. 그리고 A3 용지로 만든 종이비행기의 길이의 무게중심과 공력중심 사이의 길이에 대한 비율은 대략 (비행기 길이):(두 중심사이의 길이)= 5.4 : 1이 나왔다.
이는 A4, B4용지로 제작한 비행기에서도 비슷한 비율을 구할 수 있었기 때문에 비행거리가 가장 길은 무게중심과 공력중심 사이의 길이 비가 존재한다는 것을 확인할 수 있었다.
Ⅴ. 결론 및 제언
두 실험에서 모두 공력중심과 무게중심 사이의 거리가 멀어짐에 따라 비행거리가 증가하였다. 반면 비행거리가 최대가 되는 특정한 비율을 넘은 이후에는 궤적이 불안정해지고, 비행거리가 급격히 감소하는 모습을 관찰하였다. 실험을 통해 비행기의 공력중심과 무게중심이 더 멀리 떨어져 있을수록 더 멀리 비행해, 비행기의 길이와 공력중심, 무게중심 사이의 거리의 비율이 약 5.5:1 정도가 되는 지점에서 비행거리가 가장 멀어지며, 이보다 무게중심과 공력중심의 거리가 더 커지면 비행기의 비행이 불안정해진다는 사실을 알게 되었다. 비행기의 공력중심을 기준으로 무게중심이 더 앞쪽에 있어야 한다는 사실과 그 이유, 그렇지 않을 경우 일어날 수 있는 일들에 대해 알게 된 후, 무게중심이 얼만큼 더 앞쪽에 위치해야 하는지 의문을 제기하고 이를 해결하기 위해 직접 행동하였다는 점에서 탐구활동의 의미를 찾을 수 있다고 생각한다. 무게중심과 공력중심 사이의 거리가 일정한 비율을 넘을 경우 비행기가 안정적으로 날 수 없는 원인에 대한 탐구로도 이어질 수 있을 것이다. 공력중심에 대해 아직 구체적으로 이해하지 못했기 때문에 추가적인 자료 조사와 탐구를 통해 날개의 단면과 형태에 따라 공력중심의 계산방법은 어떻게 달라지는지 등 수업중 들었던 다른 의문에 대해서도 해결하고 싶다.
Ⅵ. 참고문헌
●Holger Babinsky, ‘How do wings work?’, in Physics Education · November 2003
●‘Aerodynamic Center’, google, https://www.flitetest.com/articles/
where-should-an-rc-airplane-center-of-gravity-be, 2023.02.27.
●‘Center of Pressure, Center of Aerodynamic’, NASA Glenn Research Center, https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/ 2023.02.28.
●’Lift’, Wikipedia, https://en.wikipedia.org/wiki/Lift_(force), 2023.03.01
●항공우주학개론 2장 비행원리, 서울대학교 기계항공공학부 김종암 교수 교육자료, https://ocw.snu.ac.kr/sites/default/files/NOTE/9534.pdf, 2023.03.01
●최누리, 종이비행기의 항공역학: 활공하는 종이비행기의 구조 안정성과 비행거리, 제 17회 NYSC 우주과학 포럼(2021.03.21.), 2023.02.25
지도 선생님 - 임미선








